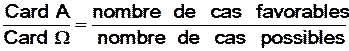Calcul de probabilités

L’Axiomatique de Kolmogorov

Le concept de probabilité n’est pas la propriété exclusive des mathématiciens, dans le langage usuel, le mot de « probabilité » caractérise la possibilité apparente d’un fait sans qu’il soit besoin d’invoquer les mathématiques pour le comprendre. .

Ce que nous apprend Kolmogorov, c’est qu’avant de parler de probabilités au sens mathématique, il faut vérifier que l’on se trouve bien dans un espace de probabilités dont les composantes, l’organisation et les règles de quantification vérifient certaines propriétés particulières.

Pour cela il nous faut :

A Une expérience aléatoire dotée d'un protocole définissant les modalités d'obtention d'un résultat (appelé issue) sous l'influence exclusive du hasard

B Un univers qui est l'ensemble Ω de toutes les issues possibles de l'expérience aléatoire

C Des évènements A _i qui sont des sous-ensembles (des parties)  de Ω

Si on appelle ℘(Ω)  l’ensemble de parties A_i de W sur lesquelles on veut exprimer une probabilité, ℘(Ω) doit vérifier les propriétés d’une TRIBU c’est à dire

 Si A _i Î ℘(Ω)   , son complémentaire, Ω privé de Ai, noté  = Ω – A _i Î ℘(Ω)

 Si on prend une suite dénombrable de classes (A₁ , A ₂ , ..A _n) , leur réunion ( U A _i ) appartient à ℘(Ω)

 L’ensemble vide noté Æ est dans ℘(Ω). C’est l’évènement impossible

D  et enfin il nous faut un procédé de mesure de la probabilité (mesure de Ai = P(A _i))  associée à tout évènement A _i de la tribu. Ce qui sous-entend que les évènements, en tant que sous-ensembles doivent être mesurables.

A ce sujet nous devons remarquer que le nombre d'éléments d'un ensemble fini dénombrable en constitue une mesure au sens mathématique et que l'ensemble des parties de Ω (si on y ajoute ∅ et Ω  lui-même) constitue une tribu sur Ω.

Dans ce cas un évènement constitué d'un seul élément de Ω  est dit élémentaire.

Mais si une expérience aléatoire adopte un tel ensemble pour univers, il faudra préciser dans son protocole qu'elle ne doit favoriser ou défavoriser aucun des éléments de cet ensemble. Autrement dit: tous les éléments de cet ensemble doivent être équiprobables devant cette expérience.

La mesure P(A _i) d'un évènement est comprise entre 0 et 1 et elle doit vérifier  certaines propriétés qui ne sont en fait que la traduction en langage mathématique du concept intuitif de probabilité, lié au concept mathématique de mesure.

 P est une application de la tribu ℘(Ω)   vers [0 ; 1 ] .        P(A _i) Î [ 0 ; 1 ]

 P(Ω) = 1  (il est certain qu’un évènement de Ω se produira)

 Si A1 et A2 sont disjoints P(A1 U A2) = P(A1) + P(A2)

      Cette propriété est aussi vraie pour une famille plus nombreuse de A _i disjoints.

Donc les évènements sont les sous-ensembles de W sur lesquels la probabilité a un sens. L’ensemble des évènements contient forcément l’ensemble vide, le complémentaire de chaque évènement et la réunion d’un nombre quelconque d'entre eux.

Propriétés de la tribu A  :

D’abord quelques dessins pour fixer les idées sur les opérations sur les ensembles.

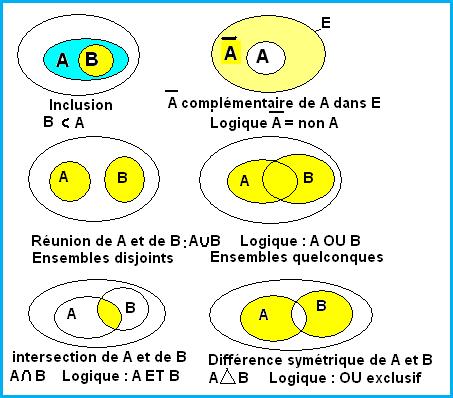Les ensembles notés A et B sur le dessin sont des évènements (peut être réduits à un seul élément mais on les imagine à priori comme en contenant plusieurs). Ce qui permet de les appeler évènements, c’est qu’on peut déterminer leur probabilité P(A) , P(B) , ainsi que la probabilité de leur réunion

P(A U B), de leur intersection

P(AÇ B) de leur complémentaire ou de leur négation P() et P( ).

A chaque opération sur les ensembles correspond un opérateur logique sur les évènements associés.

Par exemple à la  réunion de A et de B (notée A U B) correspond la réalisation de l’évènement A OU de l’évènement B . Opérateur logique OU inclusif. Ce qui signifie qu’il est équivalent de dire « je mesure la probabilité pour que A ou B se réalise » ou  « je mesure la probabilité pour que l’un des évènements contenus dans A U B se réalise » .

Aux opérateurs logique entre évènements ...

 « non Ai » est l’évènement contraire de Ai  noté

 Le Ou entre 2 évènements est exclusif quand il implique la réalisation d’un évènement mais pas de l’autre

(« vous avez le choix entre fromage OU dessert » , l’un exclut l’autre) .

Symbole du OU exclusif en logique : Å

 Le Ou entre 2 évènements est inclusif quand il implique la réalisation d’au moins l’un des évènements

(« Pour y avoir droit il faut être riche OU chanceux ».

Rien n’interdit d’être chanceux ET riche)

Symbole du OU inclusif en logique : +

 Le ET entre 2 évènements implique la réalisation simultanée des 2 évènements en un seul.

(« je suis petit ET méchant ».  Les deux à la fois). 

Conjonction de 2 ou plusieurs évènements.

Symbole du ET en logique : Le point ·

....Correspondent des opérations  sur les ensembles d’évènements.

 À l’évènement correspond l’ensemble complémentaire de A_i dans Ω noté C_Ω Ai

 L’évènement A1 U A2 est la réunion de 2 évènements. Il se produit si A1 se produit OU si A2 se produit  (ou les 2 en même temps ce qui est le signe du OU inclusif) .

On peut le noter      A1 OU A2 .

Cet évènement appartient à A.

 L’évènement A1 Ç A2 est appelé conjonction ou intersection de A1 et A2

 Il correspond à la réalisation simultanée de A1 ET A2 .

On appelle cet évènement A1 ET A2 .

 2 évènements A1 et A2 sont dits incompatibles si la réalisation de l’un exclut la réalisation de l’autre.

Ce qui signifie que leur réalisation simultanée est impossible et donc, que l’intersection de A1 et A2 est vide..

Exemple « tirer un numéro pair » et « tirer un numéro impair »  quand on ne tire qu’un numéro.

Dans ce cas le OU qui les réunit est à la fois inclusif et exclusif puisque la classe A1 et la classe A2 n’ont aucun point commun.

On dit que les ensembles qui les représentent sont disjoints (ils n’ont aucun point commun)

 L’intersection (Ç Ai ) d’une suite dénombrable d'évènements est incluse dans Ω.

Mais il arrive que cet ensemble soit vide.

 On dit qu’un évènement (ou une classe) A1 est inclus dans A2 , ce qu’on note

A1 Ì A2 quand la réalisation de A1 implique la réalisation de A2 .

L’ensemble A1 est tout entier contenu dans  A2

Propriétés de la probabilité

P(Æ) = 0 .

La probabilité d’un évènement impossible est nulle.

P() = 1 – P(A _i) .            

                  On a U A_i = Ω   et ces 2 classes sont disjointes d’où

P() + P(A _i) = P(Ω) = 1

Si A1 Ì A2   alors P(A1) ≤ P(A2)

       Plus l’ensemble d’évènements croît dans Ω plus (à priori) sa probabilité augmente.

Dans le cas général : P(A1 U A2) = P(A1) + P(A2) – P(A1 Ç A2)

          Les évènements de A1 Ç A2 sont comptés 2 fois dans A1 et dans A2

Exemples  d’espaces de probabilités

On tire une boule dans une urne qui  contient 3 boules jaunes et 5 rouges.

 Une boule est un évènement élémentaire.

    En tout il y en a 8 possibles : « tirer la boule no 1, tirer la boule no 2, …tirer la boule no 8 »

 Tirer une boule noire est un évènement impossible.

 L'évènement correspondant à "tirer une boule jaune" est l'ensemble A1 des 3 boules jaunes (Par exemple B1 , B5 , B8)

 L'évènement correspondant à "tirer une boule rouge" est l'ensemble A2 des 5 boules rouges (tirer B2 , B3 ,B4, B6 ou B7 réalise cet évènement)

  Je tire une boule. Elle est rouge ou jaune.

Mais l’évènement tirer une boule jaune ET tirer une boule rouge est impossible puisque je ne tire qu’une boule. Cet évènement ne se produit jamais.

L’intersection de  2 évènements est nulle. Les évènements tirer une boule jaune et tirer une boule rouge sont incompatibles.

 Par contre non seulement l’évènement tirer une boule rouge OU tirer une boule jaune a un sens mais il se produit a tous les coups (puisqu’il n’y a que des boules rouges ou des boules jaunes) .

L’évènement Tirer une boule jaune est la réunion de 3 évènements élémentaires : tirer B1 ou tirer B5 ou tirer B8

On achète un billet de loterie parmi une série de 100 numérotés de 00 à 99.

 Un numéro de  billet est un évènement élémentaire.

 Un numéro de billet se terminant par un 5 est un évènement contenant les évènements élémentaires suivants : « le 05 , le 15 , …….le 95 » en tout 10 possibilités.

 Acheter un billet  commençant par un 2 est un évènement contenant les évènements élémentaires suivants : « le 20 ,  le 21 , …….le 29 » en tout 10 possibilités.

 « Acheter un billet  se terminant par un 5 ET commençant par un 2 »  est un évènement de la tribu. Un seul cas correspond à cet évènement : on  a acheté le 25. L’intersection  (ou conjonction) des 2 évènements n’est donc pas nulle et les évènements « acheter un billet se terminant par un 5 » et « acheter un billet commençant par un 2 » ne sont pas incompatibles. Ils peuvent se produire simultanément.

 « Acheter un billet  se terminant par un 5 OU commençant par un 2 »  est un évènement de la tribu.

Il y a 19 billets dans cet évènement. (on ne compte le 25 qu’une fois) .

 « A1 = acheter un billet se terminant par un 3 »implique « A2 = acheter un billet se terminant par un nombre impair » A1 Ì A2.

Il faut donc distinguer l'évènement que constitue l'avènement d'une issue vue par l'observateur qui est caractérisé par un verbe par exemple "tirer une noire, avoir les cheveux bruns, mesurer plus de 1m50, …" et l'évènement au sens des probabilités qui est un ensemble d'issues, l'ensemble des issues qui réalisent l'évènement sur lequel spécule l'observateur.

Exemples de probabilités

Achat d’un billet de loterie sur 100.

Il y a 100 évènements élémentaires possibles (autant que de billets)  dans Ω.

On décide que tous ont la même probabilité p (évènements équiprobables)

Et comme tous sont indépendants. On a

P(Ω) = 1 = 100p d’où on déduit que p = 0.01 . La probabilité d’acheter tel billet est 1/100.

Par exemple probabilité d’acheter le billet no 25     P(25) = 1/100

La probabilité de l’évènement impossible par exemple acheter le no 150 : P(150) = 0

Billet se terminant par 5 : P(X5) =  P(05) + P(15) +…+P(95) = 0.1 = 1/10

Billet ne se terminant pas par 5 : P() = 1 – 0.1 = 0.9 = 9/10.

Billet commençant par 2 : P(2X) = P(20) + P(21) +…..+P(29) = 0.1= 1/10

Billet commençant par 2 ET finissant par 5 = P(2X Ç X5) = P(25) = 0.01

Billet commençant par 2 OU finissant par 5 :

P(2X U X5) = P(2X) + P(X5) – P(25) = 0.2 – 0.01 = 0.19

Pourquoi  – P(25) ? Parce que le billet no 25 est compté 2 fois dans P(2X) et dans P(X5).

(on peut vérifier qu’il y a 19 billets dans la classe 2X U X5 ) .

Billet impair (un sur deux)    

P(impair) = P(X1) +P(X3)+P(X5)+P(X7)+P(X9) = 5 (0.1) = 0.5 = ½ .

Billet se terminant par 3 Ì billet impair   P(X3) = 0.1 et  P(impair) = 0.5

On contrôle que P(X3) ≤ P(impair) normal puisque

{impairs} = {X3} U {X1  U  X5  U  X7 U X9}

En gros on peut dire que la définition de cette probabilité est inhérente au fonctionnement de la machine ou du programme qui imprime les billets. C’est la machine ou le programme qui sont garants de l’intégrité du lot de 100 billets, de la similitude d’aspects des billets, de la répartition équitable des chiffres des dizaines et des chiffres des unités sur les 100 bouts de papiers semblables qui vont être proposés aux joueurs. 

La probabilité découle de la connaissance exhaustive de l’ensemble des billets.

Probabilités et statistiques.

Nous étudions un échantillon assez nombreux de la population, mettons 20000 personnes prises au hasard, selon deux caractères

 l’état civil e (marié, célibataire, veuf)

 le nombre n de télévisions possédées (l’étude dévoile que 0 ≤ n ≤ 4)

C’est ce que l’on appelle une étude croisée.

Pour une personne donnée je note (e , n) le couple trouvé. Par exemple (c , 1) correspond à une personne célibataire possédant 1 téléviseur.

L’étude nous permet de compléter le tableau suivant par les fréquences en fonction des 2 caractères :

N e	0	1	2	3	4
c
m			F(m,2)
v

Par exemple, à l’intersection de la ligne m et de la colonne 2, j’aurais la fréquence de la population mariée avec 2 télés F(m,2).

Pour avoir la fréquence de « marié » F(m) il me faudra faire la somme des fréquences de la ligne m .

Pour avoir la fréquence de « 2 télés » F(2) il me faudra faire la somme des fréquences de la colonne 2.

Je peux considérer que F(m,2) est la fréquence de ceux qui sont mariés ET  qui ont 2 télés.

C’est donc l’intersection de la classe (m) et de la classe (2).

Pour avoir la fréquence de 1 OU 2 télés F(1 ou 2) je ferai la somme des fréquences de 2 premières colonnes.

C’est la réunion de 2 classes.

(1) et (2) sont incompatibles  F (1 ET 2) = 0  les 2 colonnes n’on aucun point commun

Pour avoir la fréquence de ceux qui n’ont pas 4 télés F() j’ajouterai les fréquences des 4 premières colonnes.

C’est la classe complémentaire de la classe 4.

Les lois statistiques nous disent que lorsque nous avons pris un échantillon assez nombreux, les fréquences que nous mesurerions dans le population globale, ne seraient pas très éloignées de celles que nous avons mesurées dans notre échantillon.

On voit bien par ailleurs que les classes étudiées, si on leur ajoute l’ensemble vide, forment une tribu et que la fréquence (en tant que chiffre compris entre 0 et 1 affecté à chaque classe) peut très bien jouer le rôle d’une probabilité.

Il n’est donc pas incorrect au sens de Kolmogorov, si nous rencontrons une personne au hasard, de dire que :

 la probabilité pour qu’elle soit mariée est F(m)

 la probabilité pour qu’elle ait 2 télés est F(2)

 la probabilité pour qu’elle soit mariée avec 2 télés est F(m,2)

Tous ces chiffres étant extraits du tableau constitué lors de notre étude. 

Ici, la probabilité ne découle plus de la connaissance d’un processus ou d’un programme structurant un ensemble selon des lois précises, mais de l’étude d’une population qui  permet de mesurer les fréquences de modalités de certains caractères, ces fréquences étant assimilées à la probabilité pour que le caractère prenne la modalité correspondante.

La loi qui fait correspondre les fréquences aux modalités est appelée loi de répartition du caractère selon ses modalités (il peut s’agir de la loi de répartition d’une variable aléatoire selon ses valeurs) . La connaissance de cette loi peut découler d’un mécanisme ou d’un recensement. Peu importe, dans tous les cas, la connaissance de cette loi de répartition équivaut à la connaissance d’une probabilité.

PROBABILITES TOTALES

 Dans tous les cas

                  P(Ω) = 1

                 P(Æ ) = 0

P() = 1 – P(A)

 Si A et B incompatibles (A et B ne peuvent être réalisés en même temps)

             P ( A et B ) = 0   

P(A OU B) = P(A) + P(B)

 Si A et B compatibles

             P ( A et B ) ¹ 0   

P(A OU B) = P(A) + P(B) – P(A et B)

 Si tous les évènements élémentaires sont équiprobables (tous ont par définition  la même probabilité)

            P(A) =

Card A et Card Ω = nombre d’évènements élémentaires contenus dans A et dans Ω.

              On utilise souvent l’analyse combinatoire pour dénombrer les ensembles et calculer Card A

Exemple jet d’un dé à 6 faces : 

Soit X le chiffre figurant sur la face exposée du dé.

Les possibilités formant Ω sont X = 1 , X = 2 , X = 3 , X = 4 , X = 5 , X = 6

 P ( 1 ≤ X ≤ 6) = P(Ω) = 1

 Si tous les évènements sont équiprobables et que leur probabilité est p on a 6p = 1 d’où p = 1/6 .

            P(X=1) = P(X=2) = … = P(X=6) = 1/6

 P (X =7) = 0    ( X  = 7 ne fait pas partie de Ω)

 P (X ¹ 5) = 1 – P(X = 5) = 1 – 1/6 = 5/6

 X = 1 et X = 2 sont incompatibles puisqu’on ne jette qu’un dé d’où

       P (X = 1 ET X = 2) = 0

       P(X = 1 OU X = 2 ) = 1/6 + 1/6 = 2/6

 X pair et X multiple de 3 ne sont compatibles

        P (X pair) = P(X = 2 ou 4 ou 6) = 3(1/6) = 3/6 = 1/2

        P (X multiple de 3) = P(X = 3 ou 6) = 2(1/6) = 2/6 = 1/3

        P(X pair ET X multiple de 3) = P ( X = 6) = 1/6

        P(X pair OU X multiple de 3) = P(X pair) + P(X multiple de 3) – P(X = 6)  = 1/2+1/3 –1/6 = 4/6 = 2/3

 cas favorables / cas possibles

Card (Ω) = 6   (6 cas possibles pour X)

Si A est l’évènement  X ≤ 4 , le Card (A) = 4   (4 cas favorables à X ≤ 4)

Donc la probabilité de A : P(X ≤ 4) =

PROBABILITES COMPOSEES

Reprenons l’exemple du jet de dé à 6 faces.

 La probabilité pour que X soit impair est

P(A) = P(X = 1 ou 3 ou 5) = 3/ 6 = 1/2.

 La probabilité pour que X soit ≤ 4 est

P(B) = P(X = 1 ou 2 ou 3 ou 4) = 4/6 = 2/3

 La probabilité pour que X soit ≤ 4 ET  X  impair est

P(A et B) = P(X = 1 ou 3) = 2/6 = 1/3

 Quand on sait que X est impair, (A réalisé) l’ensemble des possibles Ω subit une restriction en Ω_A

     Ω_A est composé de X = 1, X = 3 , X = 5 . En fait c’est A qui devient le nouveau référentiel.

     Dans Ω_A la probabilité de chaque évènement élémentaire n’est plus 1/6 mais 1/3

La probabilité de X ≤ 4 (évènement B) quand on sait que X est impair  (A réalisé) est dans ce nouveau référentiel :

P(B \ A) = P(X = 1 ou 3) =     2/3

P(B \ A) se lit probabilité de  B quand A est réalisé (notation possible P_A(B)).

                             Ou probabilité conditionnelle de B (conditionnée par la réalisation de A)

On remarque que  P(B \ A) = =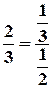

Cela s’explique de la façon suivante :

Quand A est réalisé, c'est lui qui devient l'univers et P(B\A) n'est jamais que la comparaison de la mesure de B∩A (restriction de l'évènement B à A) et de A.

Donc si m(B∩A) et m(A) sont les mesures de ces évènements on a

P(B\A) =

Probabilités conditionnelles (cas général)

P(B \ A) =                 ou            P(B et A) = P(A) . P(B\A)

2 évènements sont dits indépendants si la réalisation de l’un ne modifie pas la probabilité de l’autre. 

Probabilités conditionnelles (évènements indépendants)

2 évènements sont dits indépendants si   P (B \ A)  = P(B)

Ce qui signifie que la réalisation de A n’a aucun impact sur la réalisation de B et qu'on peut comprendre comme "la fréquence de B dans A est la même que la fréquence de B dans l'univers Ω".     

Quand les évènements sont indépendants, on a

P (A ET B ) = P(A) . P(B)

  On distribue au hasard 52 cartes à 4 joueurs. Chacun en a 13.

La probabilité pour que le ♥R soit dans le jeu de Paul est  P(B) = 13/52 = ¼ .

La probabilité pour que La ♥D soit dans le jeu de Paul est P(A) = 13/52 = ¼

Mais la probabilité que le ♥R soit dans le jeu de Paul quand la ♥D y est déjà n’est plus que de

P(B\A) = 12/51 car la ♥D occupe une place vacante dans le jeu de Paul (il n’en reste plus que 12 au lieu de 13) et il ne reste plus que 51 cartes disponibles pour prendre une autre place.

Donc les évènements A et B  ne sont pas indépendants.

On a P(♥R et ♥D dans le jeu de Paul) = P(♥D dans le jeu de Paul ). P(♥R quand la ♥D y est)

P (A ET B) =   P(A) . P(B\A) =

Confirmons par un autre procédé de calcul

Tous les jeux possibles pour Paul sont de la forme XXXXXXXXXXXXX 13 cartes quelconques parmi 52.

Il y  a  jeux possibles pour Paul

Tous les jeux favorables à l’hypothèse ♥R et ♥D dans le jeu de Paul sont de la forme

♥R ♥D XXXXXXXXXXX où les 11X sont quelconques parmi les 50 cartes qui ne sont pas  ♥R ou  ♥D . Cela fait   combinaisons. favorables.

La probabilité de ♥R ♥D chez Paul est donc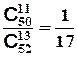

 On lance 2 dés à 6 faces.

La probabilité que le dé A donne un 6 P(A = 6)  est 1/6.

La probabilité pour que le dé B donne un 5 est P(B =5) = 1/6.

La probabilité pour que le dé B donne un 5 quand le dé A a donné un 6 est toujours P(B \ A) = 1/6.

On a donc P(B \A ) = P(B)

Les évènements A et B sont indépendants.

Dans ce cas, la probabilité pour que le 1^er dé donne un 6 et le second un 5 est :

P(A = 6 et B = 5) = P(A = 6) . P(B = 5) = 

PROBABILITE DES CAUSES : Loi de Bayes

Supposons qu’un espace de probabilités soit partitionné selon 2 caractères  correspondant à des évènements dont les modalités sont exclusivement : 

A et  , B et

Cela revient à dire que notre espace est partitionné en 4 classes (4 évènements) 

A B  ,   A ,   B   ,

Supposons maintenant que selon A ou  la probabilité de B ou  soit radicalement différente.

Par exemple l’évènement B se produit plus fréquemment quand l’évènement A (ou )  s’est produit.

Cela revient à dire que A (ou ) est une cause de B.

On connaît la relation de cause à effet quand on connaît

La probabilité ou fréquence de A qu’on appelle p

(La probabilité de de est donc 1–p)

La probabilité P(B \A) =  q . Probabilité de B quand A s’est produit

(Donc P ( \ A)  = 1 – q )

La probabilité P(B \ ) =  Q . Probabilité de B quand  s’est produit

(Donc P (  \ ) = 1– Q )

On peut représenter cette situation dans l’arbre pondéré suivant :

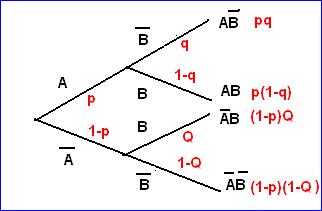
À droite la partition de notre espace de probabilité  avec la fréquence de chacune des 4 classes présentes.

Remarquons que (comme il se doit) la somme des fréquences = 1 :

pq + p(1–q) + (1–p)Q +(1–p)(1–Q) = 1

Supposons maintenant que toute trace de l’évènement A (ou ) ait disparu et que seul l’évènement B (ou  ) soit observable.

Quand on observe un évènement B (ou  ) on peut se poser la question suivante : « quelle est la probabilité pour qu’il ait pour cause un évènement A (ou ) ? »

Bayes nous dit comment répondre à cette question :

Supposons qu’on observe l’évènement B .

Il provient forcément de l’une des classes

A B p(1–q)            ou    B          (1–p)Q.

Le poids total de ces classes est  p(1–q) + (1–p)Q et dans l’ensemble des 2 classes, A et  sont probables en proportion du poids de leur classe.

On a donc

P (A\ B) =              et  P (\ B) =  

La somme de ces 2 probabilités est bien 1 .

p(1–q) + (1–p)Q  est la fréquence ou probabilité de B dans l’ensemble observable P(B).

p(1–q)  est P(A) . P(B \A)

On a donc

P(A et B)=

Si on observe l’évènement  on raisonnera de façon identique à partir des 2 rameaux extrêmes de l’arbre, ceux des classes qui contiennent  soit :   A et

Exemples BAYES

 Les machines à laver sont produites à 60% par l’usine A et à 40% par l’usine B .

L’usine A produit 7 machines défectueuses sur 10.000. L’usine B en produit 1 sur 10.000.

Nous achetons une machine défectueuse. Quelle est la probabilité pour qu’elle provienne de l’usine A ?

P(A) = 0.6 , P( ) = 0.4

P(défaut \ A) = 0,0007

P(défaut \ ) = 0.0001

P(défaut )  = 0.6 x 0.0007 + 0.4 x  0.0001 = 0.00042 + 0.00004 = 0.00046

P(A \ défaut) = 0.00042 / 0.00046 = 91% .

 La fréquence d’un gêne G dans la population est 40% .

La probabilité d’attraper une maladie M quand on est porteur du gêne est 70% , dans le cas contraire cette probabilité est de 20%.

Quelle est la probabilité pour qu’un malade de M soit porteur du gêne G ?

P(G) = 0.4 

P(non G) = 0.6

P(M) = 0,4 x 0,7 + 0,6 x 0,2 = 0,28 + 0,12 = 0,4

P(G \ M) = 0,28 / 0,4 = 70%.